To Confirm the Original 44.1kHz/16bit Format
It is exciting to create something new. Some people just grab a soldering iron, others deliberately start a simulation. Everyone seems to have his/her own approach. In my case, it starts with going back to the basics, research the history, and re-construct the whole picture in my mind. On starting this project I did research as many resources as I could put my hands on.
As the new generation of CD format is appearing on the horizon, I thought the basic concept should be "To Confirm the Original 44.1kHz/16bit Format". A CD in our hands has exactly the same data, every bit to bit, as to the one that left the studio. To recall this dreamy fact, the above theme would be quite appropriate. Any high-bit or high-sampling does not have its raison d'être unless it surpasses this level of accuracy.
About Non-Oversampling
After examining the following two aspects, I came to a conclusion that 'it is quite difficult to carry out oversampling as theoretically under the current technology'.
1) Oversampling and Jitter
There are two axes on digitizing the sound. The time axis and the amplitude axis. In case of CD, they are 44.1kHz and 16bit. In other words, we have to press in the amplitude data into one of the 16bit stage at every 22.7 s. That produces maximum of +0.5 LSB error, and the digital audio starts by accepting this error at the beginning. However, this error only concerns the amplitude axis and no amount of error was admitted on the time axis. Let me suppose that the accuracy of 16bit means how accurately the acoustic energy (time x amplitude) is transmitted by being distributed into each steps of 16bit. Then, by making the amplitude data more accurate, we can distribute the error onto the time axis.
If we distribute 1/2 of the error,
1 ÷ 44.1kHz ÷ 2 16 ; ÷ 2 = 173 (ps)
This represents the maximum limit of the acceptable error (maximum limit of the jitter). (diagram 1)
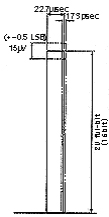
[diagram1]
acceptable error of 44.1/16bit
|
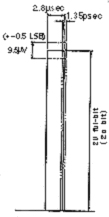
[diagram2]
acceptable error of 8 x sampling/20bit
|
All of the above is based on the basic sampling rate. When in 8 x oversampling and 20bit, that number would be 1.35ps (diagram 2). This is a totally impossible number to achieve for a separate type DAC which has to recover the clock by PLL. This means that under an average jitter environment, the oversampling can not operate theoretically, and lowers the accuracy within the operating field. In short, just by oversampling the original data, 16bit accuracy can not be satisfied anymore.
2) Oversampling and High-Bit
Originally, oversampling was developed to allow the use of an analog filter with gentler characteristics as a post-filter, and not to increase the amount of information. Many people still misunderstand this.
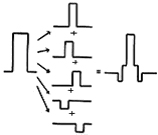
[diagram3]
principle of FIR type digital filter
|
The principle of the most popular FIR type digital filter is to shift the original data and overlay them together, not to create an additional one (diagram 3).When it overlays the data by multiplying the coefficient to the original data, there appears new information below 16bit and to recover this finer information, we need a higher bit rate processing.
|
For example, in case of a high-performance digital filter SM5842, this processing is done in 32bit and the filter round them up to 20bit to the output, creating more errors in the re-quantizing process. Recently, this problem was dealt with and a filter was created which can produce 8 x sampling all at once. But even with that, as long as you can't output the internal word length as it is, there's no way you can prevent the errors to occur.
|



